Property-Based Testing for Temporal Graph Storage

A motley of functional techniques to allow isomorphic and deterministic graph generation
Written by Igor Loskutov. Originally published 2023-12-05 on the Monadical blog.
Problem scope
We’ve all been there. You take your introverted friend to a party, and they get all soggy and sad after just half an hour. How to keep them cheerful and fresh throughout the whole event? The answer is not to overload them with social interactions. Instead, you carefully calculate their path through the house, giving them time and space to cool down, and apply social encounters in a carefully administered way. To do this like an engineer, you need the plan of the house, the position of each person at the party, and their compatibility with your friend to build an optimal social-pressure-free experience for your friend to get healthy socialization and not get drained of energy.
This is exactly1 the kind of problem that our client wanted to solve using a graph database.
A graph database is a type of database that stores data as nodes and edges, representing entities and their relationships, whereas a social graph is a graph that models the social connections between people or other entities.
But our client had a very challenging and unusual requirement: they wanted to be able to query their social graph not only for the present moment but also for any point in the past (yesterday, last month, last year, ten years ago), with high accuracy and performance. This meant that their graph database had to support temporal queries, which are not common in most graph databases.
To make things even more complicated, their social graph was very dynamic, with frequent changes in the nodes and edges. Like real-life Facebook drama, people would often “unfriend” each other, creating different shapes and patterns in the subgraphs of their social network.
How to even begin testing such a complex system? We implemented tests. And then more tests. Specifically, we implemented property-based tests that run once every time our branch is updated, a technique that generates random inputs and checks that the system satisfies certain properties (ex: only one friendship can exist between two people at any point in time). And then, I wrote about it here.
If you aren’t familiar with the concept of property-based testing, it is a way to test your code with random inputs. You use a tool that creates inputs for you and checks that your code works as expected for all of them. You also define properties, which are things that should always be true about your code, no matter the input. For instance, instead of a predetermined string “Alice”, the test suite will run the code with inputs “Bob”, “”, “ “, “Alice “, and whatnot. The same goes for integers and floats. 0, 100, MAX_INTEGER, -1, 1.00000001 are the corner cases you might expect your property-based test to generate.
But wait, there’s more. Our input is not just random primitives. It’s random graphs. We generate random graphs with nodes and edges, representing people and their relationships, and feed them to our graph database. Then we check that the database can handle historical queries on these graphs, without breaking or slowing down.
The requirement to be historical also makes our graph system an event sourcing that stores its aggregates for every event, the aggregate being the whole graph.
And it gets more interesting. The randomness in property-based testing is not really random. It’s deterministic, which means we can control it and reproduce it. Property-based testing tools tell us the seed they use to generate the random inputs, so we can run the same exact test again if we need to. And we do need to.
Why? Because we want to keep track of how our system performs over time. After each test, we save some metrics and analytics to spot any anomalies or issues later, but we can’t save the whole graph for each test because that would be far too much output. And trust me, we have a lot of output.
How much? A lot. A huge amount. The temporal graph feature is so critical for our client’s business that we can’t afford to miss any bugs or errors. So we run our tests all day, every day. And not just on one machine, but on several machines in parallel. The amount of data we generate is staggering, so if we don’t optimize it, we’ll run out of storage space in no time.

That’s why I want to focus on the graph generation process in this article. It’s a fascinating and challenging problem that deserves its own attention, whereas the details of the tests themselves are another story (which is outside the scope of this article, but which I may tell you about some other time).
I’ll show you some cool2 and unorthodox ways of generating graphs. Specifically, I’ll look at graphs that have the same formal requirements as the generated properties in property-based testing. I’ll do this with the help of state monad, newtypes, isomorphic/lazy code and some other concepts I’ll introduce you to.
You may or may not use those in your daily job, but it’s always nice to know diverse concepts to enrich the spectrum of your toolkit and your intuition.
And I just think that it’d be selfish of me not to share my findings.
Definitions
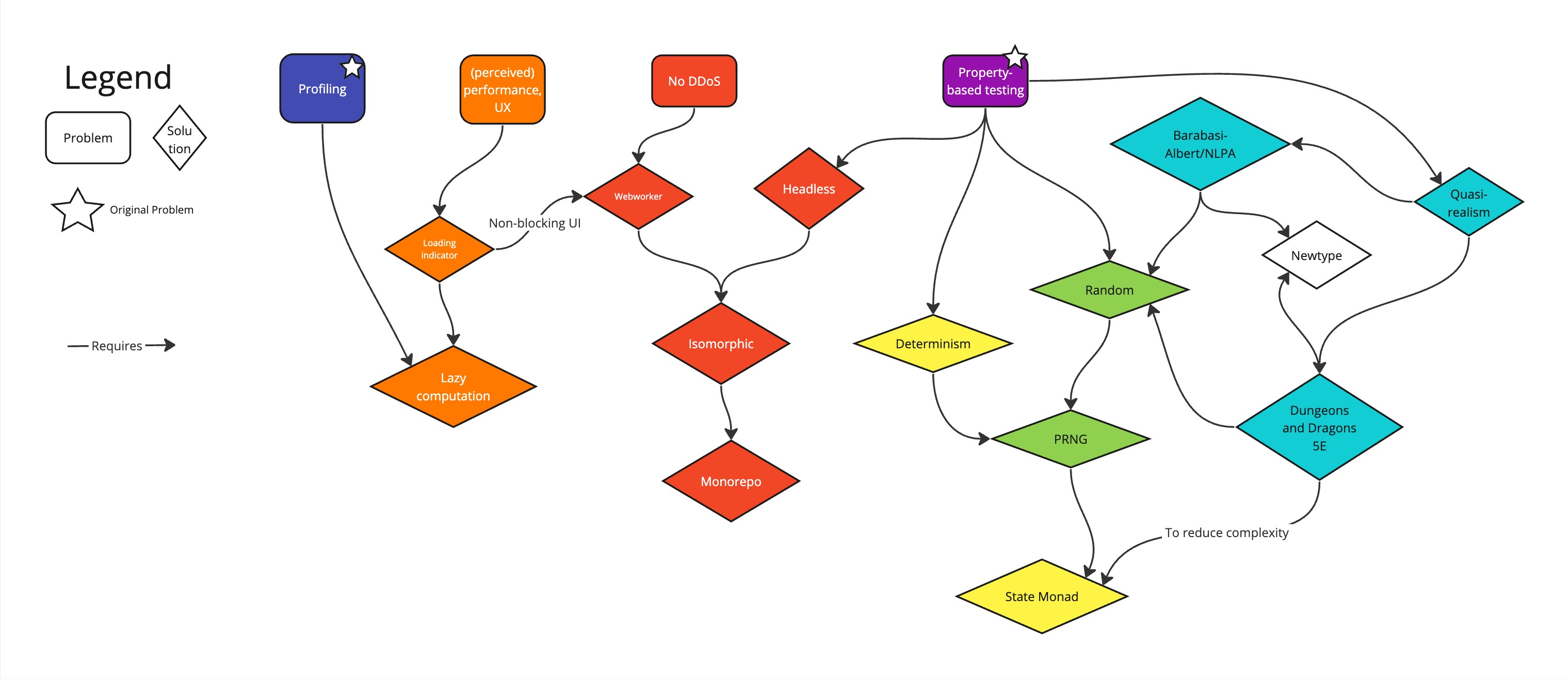
First of all, I’m going to colour-code some words; this should make it easier to distinguish each unique challenge of the task and to link those challenges with the terminology used. I’ll also explain how each requirement/solution is important and how it’s implemented.
In the picture below is a general outline of all the problems and solutions that I’ll cover. Also, notice that some solutions morph into “problems” that require their own solutions, which I’ll deal with as they arise.
In the text below, I’ll highlight the terms and their synonyms/anything related to a specific problem/solution with an appropriate colour. You can always backtrack to this diagram and look up which part of the problem/solution spectrum I’m talking about.
So, without further ado, let’s implement what I call an isomorphic* lazy** deterministic*** random**** (pseudo-random) quasi-realistic***** artificial social graph generation process.
I’ll use TypeScript for this task. It has a nice maintainability/adaptability balance, and it lets me share a lot of logic between the front end and the back end. Later, you’ll see that it goes along with the idea of client-side widgets in this article really well.
First, let’s break down this definition.
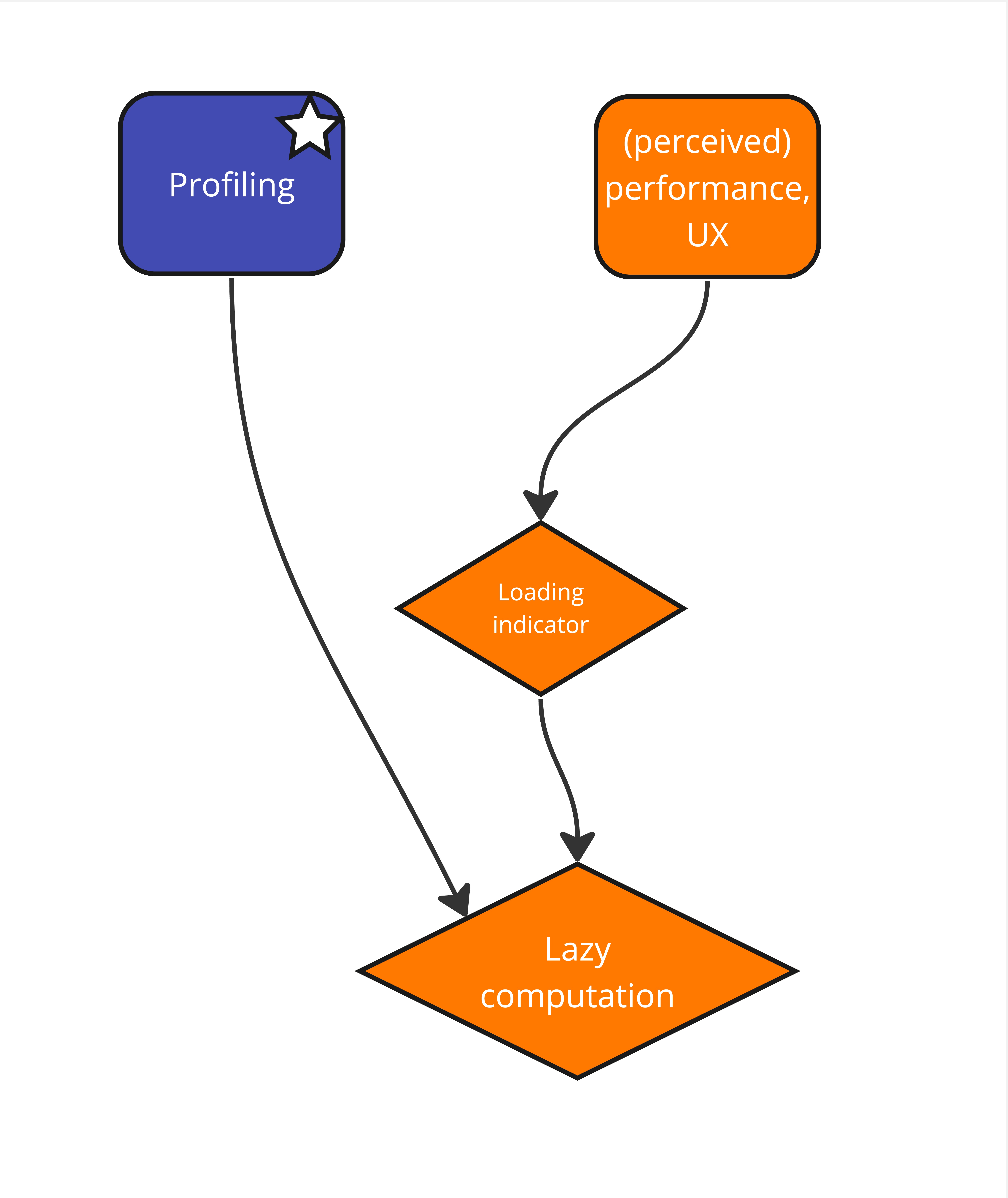
Isomorphic means that the program is able to run both on the “server” (i.e., a Node.js process) and on the “client” (i.e., browsers, both in a main thread and in a web worker). Why? I want to provide you, dear Reader, with the bliss of rendered generated graphs on this page, but I don’t want to DDoS my servers while doing it. Therefore, although the Isomorphism of this code was not an original requirement, it’ll be nice to have it.
Laziness in this context means that the computation is prepared and ready to run only when it needs to, i.e., when the next random graph is requested.
Laziness turned out to be about user experience as well. In implementing it, I made an interesting observation: having a simulation giving you its completion status (i.e. “50% completed”) improves the UX, at least for me. However, the initial purpose of laziness was the graph generation duration profiling34.
I also realized that laziness is crucial for the computation to be poll-based and not push-based. The test process involves both a stream of generated graphs and a stream of database writes, and the latter is much slower. I don’t want the generator to spam us with graphs and take a lot of CPU resources from the process.
The lazy evaluation also feels faster from a UX perspective, because the user sees the loading indicator.
Determinism is the core of the whole operation. Since I’m about to use the code for the property-based testing of my algorithms, it’s important for me to have my test cases easily reproducible. To have this, I want the generated graph to be absolutely the same in every detail to the input of the generative process. And determinism lets me have easily reproducible test cases.
Note, however, that the test cases themselves won’t be covered in this article since it strays into NDA content and is also not crucial for the topic. Note also that although I could have my code non-deterministic and get by with saving the whole graph generated — so, output instead of input — this hack turns out to be direly impractical, making me save 1+mb of a graph for each set of inputs. Having the calculation non-deterministic would also make this article less exciting!
Randomness, or rather pseudo-randomness, shares the same purpose as determinism above. I need my test cases to generate different outputs for the same set of parametric inputs, but I need to control this randomness with an initial seed given to the graph.
Quasi-realistic means that I want my graphs to be life-like. Our social graphs have a very distinct property: some of its nodes accumulate many more edges than others. In networks like this5, “the rich get richer”. Those graphs are also allowed to have cycles6.
Note that in my case, the graphs are directional; we could work with non-directional graphs the same way, though.
The first graph of our rogue gallery, “organic-medium”, where we simulate “the rich get richer” approach with the Barabási-Albert nonlinear preferential attachment model.
What is not in scope
Graph generation Performance isn’t the greatest concern because bottlenecks lie elsewhere, although the generation -> force simulation -> rendering pipeline seems to be performant enough to work with in real time. I’m sure it’s possible to make the pipeline more performant, i.e. using pure generators with imperative code, or getting rid of Laziness* entirely. The current bottleneck, though, is certainly database I/O and computations inside the database itself.
Code complexity isn’t a priority, although it’s nice to have. Because the task at hand is not standard, I also kept my mind open to unorthodox approaches to explore how it can be done in better ways. For instance, you’ll see that newtypes (which I’ll talk about later) have complicated readability quite a bit.
Solutions Outline
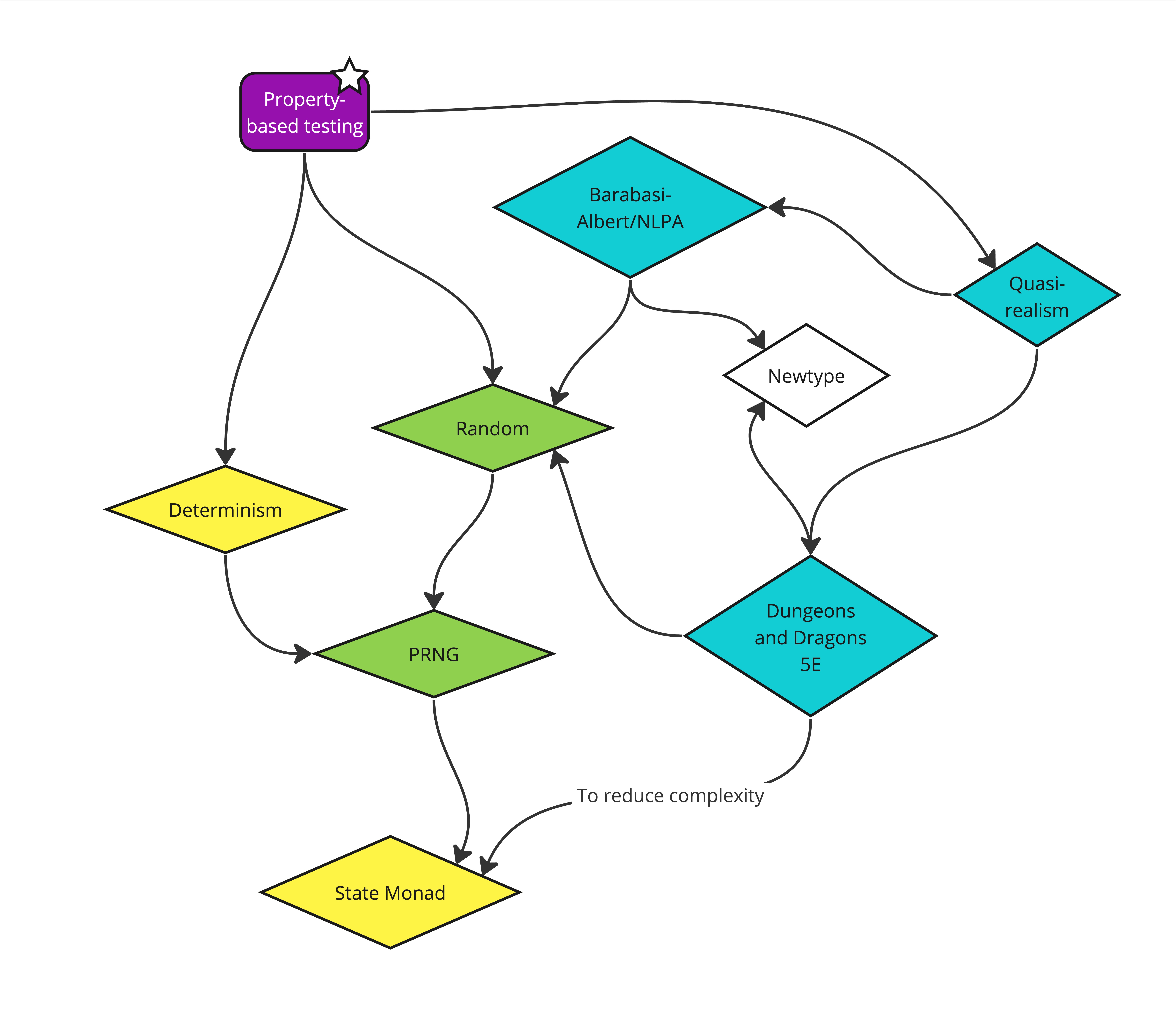
So the main problem is to deterministically generate quasi-social graphs. This problem imposes multiple requirements that consequently spawn their own problems with themselves. Laziness, quasi-realism, isomorphism, and determinism are the properties that were deemed important for the task at hand.
Lazy evaluation isn’t standard practice in Javascript7, although it is supported by the language.
We’ll try to do both lazy and functional here. Functional programming seems to be a good model for this case because the main characteristic of the whole computation is functional purity8. Even the side effect of writing into the database looks more-or-less “pure-ish” because the database is effectively re-created for each test. The generation algorithm is also lazy because we want to see the graph generation progress (and potentially, in future, set it into one big lazy pipeline with forceatlas2 layout simulation).
Lazy evaluation solves my profiling problem and also lets me organize the computation to work in polling mode. With graph generation in Node.js, it’s especially important because the generation process tends to take over the whole main thread, and unless managed properly, it is a black box until a large bunch of its execution is done. This problem is purely development/technical but is nice to solve nevertheless.
It was also important to make the generation process pausable/resumable because certain IO bottlenecks existed in my case, primarily Database IO and Web Socket IO (which I won’t delve into in this article).
Additionally, I want the code to be functional to help with deterministic behaviour. Determinism is important in this case because it allows me to eventually repeat the computation exactly as it happened, even if randomness was involved. Remember, we store metrics of each execution, and the execution output is huge without determinism.
Going functional is not necessary here, and we can achieve determinism without it, but with PRNGs, it turned out to be a very convenient way to organize computation.
I’ll solve the functional part with an iconic State Monad pattern implemented in Giulio Canti’s fp-ts library. And by using a lesser-known fp-ts-stream library, I hope to help myself with laziness.
I’ll sprinkle it with a NewType pattern to help us with arithmetic. I noticed that a lot of arithmetic types in the code are constrained, i.e. “can be only 0 to 1” or “can be only a positive integer”. Many of them are not combinable either; we can’t multiply graph Density and Heterogeneity, as that won’t make sense! (Well, in most contexts, at least). For more intuition, I invite you to read Yuri Bogomolov’s article about primitives. I’ll use newtype-ts implementation here.
I also want the graph layout to be memoizable9. This is a small detail but it helps your device battery while you load this article; it doesn’t need to do all these layout computations!
Furthermore, I’d like the generator code to be isomorphic, running both frontend and backend. Running it on a web worker with a loading indicator has proven to be a great UX. Running it on the server is a part of the original requirement of the code, where we’d want to run it headless 24/7. It’s quite easy to achieve in TypeScript. You have Workspaces and a plethora of monorepo solutions to share code between systems. I’ll use Nx here.
I also want to generate life-like graphs that potentially reflect the real social connection network. I’ll use the non-linear preferential attachment branching model, a special case of which is the Barabási-Albert model. I’ll also use a straightforward brute force Dungeons and Dragons Fifth Edition Core Rulebook10 model adaptation to show how easy it is to encode even such a tricky (from an engineering perspective) algorithm when you apply the state monad.
This is a graph generated with the DnD branching model.
When solutions become problems
We have stated problems and solutions, but you may notice they intermingle a bit. This is because of the nature of our overall solution domain: it’s not a linear story (as much as we’d like to see it usually) but it is a branching tree, or rather a directed graph (with no cycles, of course!). For instance, you can see that “lazy evaluation” solves the solution “loading indicator”. It’s all right and there is nothing to be afraid of: we eventually get to the leaf, or rather the end node, whichever solution path we’ve taken.
The main focus
Basically, the process generates a hell of a lot of graphs and runs tests on them. We want to be checking our system for errors and metrics 24/7 after all.
Given that our graph database works with very specific types of graphs - social graphs - we’d like it to be performant for this particular case (remember that we collect the performance metrics of each run). We need to generate random graphs but we also want them to look like real social graphs. There is an old observation that social graphs exhibit a common trait of power law distribution. This class of networks was called scale-free11, and there is a family of algorithms for generating them randomly.
Let’s implement this algorithm. The core of it will be graph link branching heuristics. Let’s at least start and then see how soon we can end this journey.
In my implementation, graph generation has two major phases: Genesis and Abundance. During Genesis, the generative algorithm starts from a single node and adds edges and nodes like beads on a string. There is a parameter responsible for “branchiness” called Heterogeneity, which governs how “stringy” the graph will be in this phase. Two corner cases of Heterogeneity are shown below:
During Genesis, the number of nodes is always equal to the number of edges + 1.
When I reach the target count of nodes, there is an optional phase of Abundance that adds extra edges if it’s required.
In both phases, the crucial part of the generative process is “how does it choose the nodes to connect”.
The goal is to give the “rich” nodes better chances, controlling this degree of social inequality through the Heterogeneity parameter.
One elegant way of giving some nodes a better chance to obtain more links than others is non-linear preferential attachment. It’s basically a self-reinforcing biased random distribution, where the nodes that already accumulated some edges have better and better chances to obtain even more (just like capitalism, yee-haw!).
Regardless of your economic ideologies, non-linear preferential attachment works very well for our power law distribution simulation. At Heterogeneity 0.5, it boils down to the Barabasi-Albert algorithm, generating believable social graphs
I’ll guide you through the core of non-linear preferential attachment, Barabási-Albert-style.
Here, I’ll assume that we want to simulate a social graph with only one type of non-directional relation, i.e. “friends”. We’ll start with a small pre-defined graph (you’ll see that you can generate it from any point, even from scratch; it’s just more convenient to start a bit further away from it).
Let me graphically show you just a couple of steps of the algorithm:
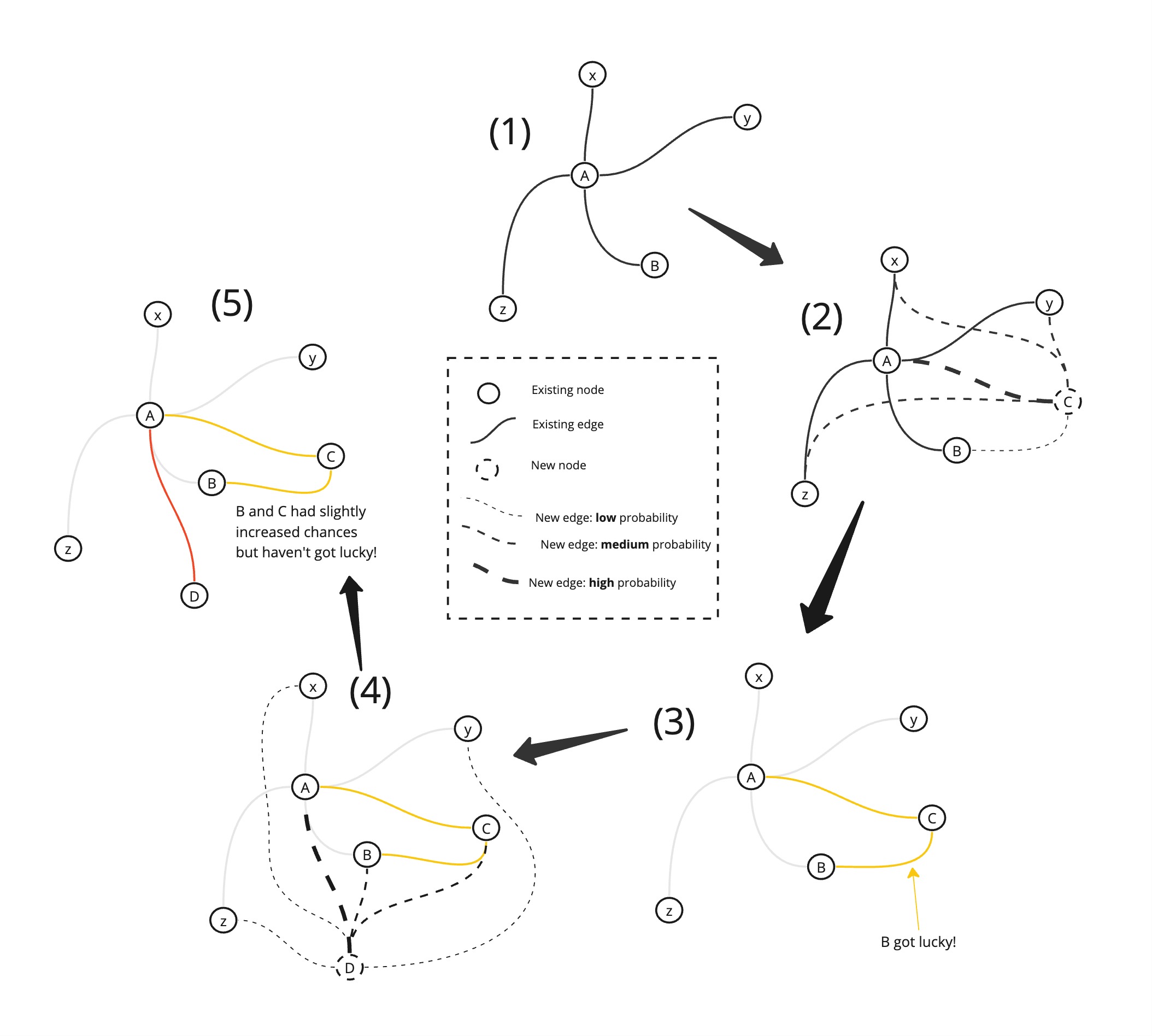
In Figure 1, there is a simple graph with one node having most of the connections. We’ll mark two nodes that are going to be significant for us as “A” and “B”. We’ll call all insignificant nodes x, y, z.
In Figure 2, we add a node (“C”) to the graph: here, our task is to determine what connections (edges) it will form with the existing nodes. In this case, the probabilistic model kicks in. For every existing node we “roll the dice”, with the chances of success being higher for the nodes that have already accumulated some connections.
Note that this tactic works just as well if we were to choose only one edge to create; however, here, I have no limit to potential edges.
Let’s assume in Figure 3 that the connection A-C was formed (it had a high probability of doing so, after all), and also, very accidentally, the connection B-C was formed as well. B got lucky! Now, in Figures 4 and 5, we account for the new power balance. We give B and C better chances to form a link. Unfortunately, as we see in (5), B and C (and every other node) still weren’t lucky enough, but A formed a link again because it was already power-tripping. (Hooray to A, I guess?)
That’s it! The task is done, right? …right?
Non-random randomness
There’s a large (quite literally) inconvenience, though. The graphs generated can be large. A lot of them are being generated and tested, and a lot of those test results are being logged, which takes up a significant amount of disk space. Let’s optimize this!
We can save only the input parameters and close the case, but there’s an issue: every time a Math.random() function is called, its return value is unpredictable. Because of this, during graph generation, several runs of the same process with the same parameters would yield different graphs! How can we make randomness non-random?
Pseudo-randomness
To get a reproducible sequence that behaves like a random number sequence, Pseudo Random Number Generators (PRNG) are used.
PRNGs always require, implicitly or explicitly, a “seed” that determines what sequence of pseudo-random numbers it will yield during sequential calls. If you’ve played Minecraft12 or Dwarf Fortress, you’re probably familiar with seed world generation, when, giving a specific seed string, the game engine always generates the same game universe.
That’s exactly it. PRNGs. Deterministic13 randomness.
What the sequence generation looks like, laid out imperatively, is:
const seed = ‘123’;
const generator = new Generator(seed);
console.log(generator.next()); // always 0.123
console.log(generator.next()); // always 0.789
console.log(generator.next()); // always 0.001
That would be an implicit state stored inside the generator object. Some libraries work like this.
And yet again, we can implement it in the generative process and call it done.
But how do we pass the Generator object around? Do we keep it as a global, or do we add it to each function as an argument? Both approaches will work, actually, and both have pros and cons. The global object is easy to implement, but you won’t be able to re-run your generative processes without proper clean-up. You won’t be able to run them in parallel14 either.
So I chose to pass it around. There is another fork in the road now, though: to pass a mutable reference or somehow make the computation immutable?
We all know that mutability introduces complexity. I’m trying to avoid it at any cost. I’d rather eat a frog! But how to make a PRNG immutable?
In the example above, Generator is an object, which encapsulates both behaviour and data. And, most of the time, that’s not what we want to have in our software.
First of all, we can separate those:
const state0 = initialGeneratorState(‘seed’);
const [n0, state1] = generate(state0); // n0 is always 0.123
const [n1, state2] = generate(state0); // n1 is always 0.789
const [n2, state3] = generate(state0); // n2 is always 0.001
So far, so good. But there’s always a point when we want to pass the generator state around our functions. For instance, in one place, I want to use it to generate the probability of an edge being attached to a node, and in another, I’m using it to generate a random (not-so-random) UUID for node id.
This looks like a context to pass around through computations, and there is, coincidentally or not, a pattern out there to make it easier!
State Monad
Here, I stop for a bit and ruminate. Do we want this article to be yet another monad tutorial? I don’t! Go figure it out yourself. They’re very simple when you finally understand them!
Instead, let’s focus on usage with PRNG.
The code that invokes 16 sequential pseudo-random generator calls and combines them into a UUID looks like this:
// rng is PRNG state passed to us and is in the scope
// note how ‘rng’ (and newRng) pops in and out of the computation, never showing itself in the middle
const [rand16, newRng] = pipe(
interval(16),
A.map(() => random0255),
A.sequence(ST.Applicative),
apply(rng)
);
const newId = v4({
random: rand16,
});
return [newId, newRng];
Note about the
pipefunction: it’s just an application flattened: i.e. instead of f5(f4(f3(f2(f1(v))))) you havepipe(v, f1, f2, f3, f4, f5). This rearrangement makes it a lot simpler to work with curried functions and, as a result, with many functional programming primitives. Another way of thinking of it is immediately applied composition. (i.e. in Haskell, you’d dof5 . f4 . f3 . f2 . f1and apply it tov).
It doesn’t look as spectacular for NLPA, where I just read State and pass the new State further, but check how the DnD bruteforce lays out:
pipe(
// helper to create an array of n elements, i.e. times=3 => [undefined, undefined, undefined]
interval(times),
// here, random is a monadical computation that carries an immutable State through its input and output
RA.map(() => random), // RA is ReadonlyArray
// sequence is running those computations in sequence, one-by-one, passing the immutable RNG State through
ST.sequenceArray, // ST is State
// reduce the content of State monad (a ReadonlyArray, at this point) into a single value, which would be our RNG result (choosing highest or lowest value, depending on advantage/disadvantage chosen strategy
ST.map(RA.reduce(unit, reducer))
);
This is one of the examples of monadical computations in my graph generator, where monads help with keeping code concise and focusing on “what” I want to achieve, not “how”. Here it helps specifically with passing the immutable RNG state, which I need for the computation to stay deterministic but still reasonably random. Without it, I’d have to pass this state manually.
This code would take a times of random numbers from the passed PRNG state, reduce it to the minimum (or maximum), and pass the result along with the new state (regenerated times times) further. This logic is equivalent to Dungeons and Dragons 5E advantage/disadvantage mechanic, where you roll two dice15 and choose the largest/smallest result but scaled to “n” rolls.
And so on and so forth.
I could have managed without the state monad, but yet again, I’d very much like to have immutability built into my computations.
We have actually just covered the deterministic part of the process. For the purpose of the original main task of property-based testing, it’s more than enough. We have our parameters serializable, and we generate the seed and parameters in the test, run whatever algorithms we want, save the result of the run (not saving the whole graph) and move on.
Congratulations! Here’s a graph for you.
Don’t worry, it just has very high Heterogeneity.
A word about Newtypes
It’s worth introducing a typing pattern that I used in this program, which is about extra primitive types stringency. I call it Newtypes here, as a Haskell tribute. To show how Newtypes can be used, let’s go with an obvious example. My graph generation process has, among others, these numerical parameters:

Heterogeneity can be any decimal in [0, 1]. Density can be any decimal in [0, 1]. Nodes can be any positive integer. Or rather, a non-negative integer. I want to have a graph with 0 nodes possible, which is simply my whim.
So, Heterogeneity is a parameter of how “branchy” the graph is.
Density dictates how many more Edges the graph will have than Nodes. With a lot of edges, it becomes very dense - try it. Any value of Density higher than 0 will make the phase of Abundance possible. Density 0 means there is only Genesis.
The number of Nodes is basically how many nodes the generated graph will have.
In TypeScript, we can define it like this:
declare const heterogeneity: number;
declare const density: number;
declare const nodes: number;
Now, we can conveniently add nodes with heterogeneity:
const nodes = 1000;
const heterogeneity = 0.5;
const x = nodes + heterogeneity; // 1000.5
And even pass density instead of heterogeneity to our methods:
const doSomethingWithHeterogeneityAndDensity = (heterogeneity: number, density: number) => {}
const heterogeneity = 0.5;
const density = 0;
doSomethingWithHeterogeneityAndDensity(density, heterogeneity);
Do you think, however, that it’s just too convenient? Probably.
Let’s make our lives harder and make invalid states unrepresentable.
Because what the hell does nodes + heterogeneity; // 1000.5 even mean? The next step would be to convert 1000.5 into USD and send it to a random user. Because this action makes exactly as much sense as adding Nodes with Heterogeneity. Why can we even do that? Don’t we have, like… types to prevent it?
Should we even be able to forget the argument order in doSomethingWithHeterogeneityAndDensity and pass Heterogeneity instead of Density (and vice-versa)?
Why does the type system prevent us from passing a number to a function expecting a string, but doesn’t prevent us from passing i.e. Velocity to a function expecting Distance?
Although those questions look rhetorical, I think I can attempt to give an answer. Tooling immaturity - that’s it. The concept of “number is not a number” and “string is not a string” is, unfortunately, as it is precise, alien to the same degree.
There is even an opinion that having strings (and numbers, if you let me extrapolate) is more often than not a sign of bad domain design.
And it’s time to stop using primitives where they don’t belong!

Follow me.
export type Heterogeneity = Newtype<{ readonly HETEROGENEITY: unique symbol }, Decimal01>;
export type Density = Newtype<{ readonly DENSITY: unique symbol }, Decimal01>;
export type ListLength = Newtype<{ readonly LIST_LENGTH: unique symbol }, NonNegativeInteger>; // Nodes
And the helper types used above are:
export type Decimal01 = Newtype<{ readonly DECIMAL01: unique symbol }, NonNegative>,
whereas NonNegativeInteger and NonNegative are helper types from the library newtype-ts.
I define the runtime bridges between Newtypes and primitives like this:
const moreThanOne = (n: number) => n > 1;
const oneOrLess = not(moreThanOne);
const nonNegativeIsDecimal01 = flow(prismNonNegative.reverseGet, oneOrLess);
export const prismDecimal01 = pipe(prism<Decimal01>, apply(nonNegativeIsDecimal01), prismNonNegative.compose);
Prism is the bridge itself. It will take a primitive, ensure its bounds, and spit out the Newtype.
Sometimes, I also want to cast a primitive into a Newtype when I’m quite sure that I’m passing a correct value and ready to get an exception right in my face:
// where castToPrism is a helper function that does some mundane stuff
export const castDecimal01 = castToPrism(prismDecimal01)(
(n) => `Invalid cast, prismDecimal01 is not in range 0-1: ${n}`
);
Now we can have the previous examples from the start of this paragraph rewritten like this:
const nodes = castListLength(1000);
const heterogeneity = castHeterogeneity(0.5);
// @ts-expect-error
const x = nodes + heterogeneity; // won’t compile
const doSomethingWithHeterogeneityAndDensity = (heterogeneity: Heterogeneity, density: Density) => {}
const density = castDensity(0);
// @ts-expect-error
doSomethingWithHeterogeneityAndDensity(density, heterogeneity); // won’t compile
What’s the catch?
heterogeneity1 + heterogeneity2 won’t compile as well. They’re not primitives anymore.
We’ll have to define something like addHeterogeneities(h1: Heterogeneity, h2: Heterogeneity): Heterogeneity and use it for additions. Same for multiplication, etc. You can even use Semiring for it.
To me, that makes code more painful to read. I just wish the language had this supported at its core. It seems that without core support, we can’t have Newtype math look nice (read “use +”).
So, pros: it makes the type level or the code much more strict. Cons: it does look ugly.
I’ll continue trying to make this approach work, though, in the future. I think it has a lot of promise and is direly underappreciated. This underrepresentation even becomes a self-fulfilling prophecy: the feature is not popular; ergo, we don’t add it to the language. We don’t have the feature in the language, ergo, it’s not popular.
The lazy part
Alright, we’re really close: the Lazy part and then some technicalities.
I want to give you a loading indicator. Not only that, but I would also love to be able to see how fast my graph generation phase goes.
Let me give you some insight into the parts/phases of graph generation and representation pipeline.
First, we’d like to generate the graph, which is just nodes and edges, represented in whatever way. Adjacency List data structure is quite popular. I use one from the thi.ng toolkit (check it out - it’s fascinating).
Secondly, we’d like this data to be placed on a 2d or 3d or nd (if you’re evil) plane. Graph layout algorithms do this, and the most generic “family” are force-directed algorithms. This paper summarizes them nicely. My favourite so far is forceatlas2 because it can work with dynamically added nodes/edges, therefore, streaming. I use D3, though, for now (too much bother otherwise). There is a nice graph drawing library that does a lot out-of-the-box, and I picked it because it has nice animations and integrates D3 force layout for me; I also wanted to focus on graph generation and distinguish G6. The docs are partially in Chinese, but they do some crazy stuff with layouts, including running their computation through webgpu compute shaders. It’s just too awesome not to tell you.
The third part is to render it all, preferably with nice animations, curvy shapes and mouse interactions.
So, in the final product that you see in those iframes, only the graph generation phase is lazy. But the potential, having switched to forceatlas2, is to see graph generation in real-time, making the whole pipeline lazy.
In order to add laziness to graph generation, I went the way of event sourcing. Instead of the graph itself, the algorithm produces the events “node added” and “edge added”. Those are collected into a graph data structure before being fed to the Layout simulation.
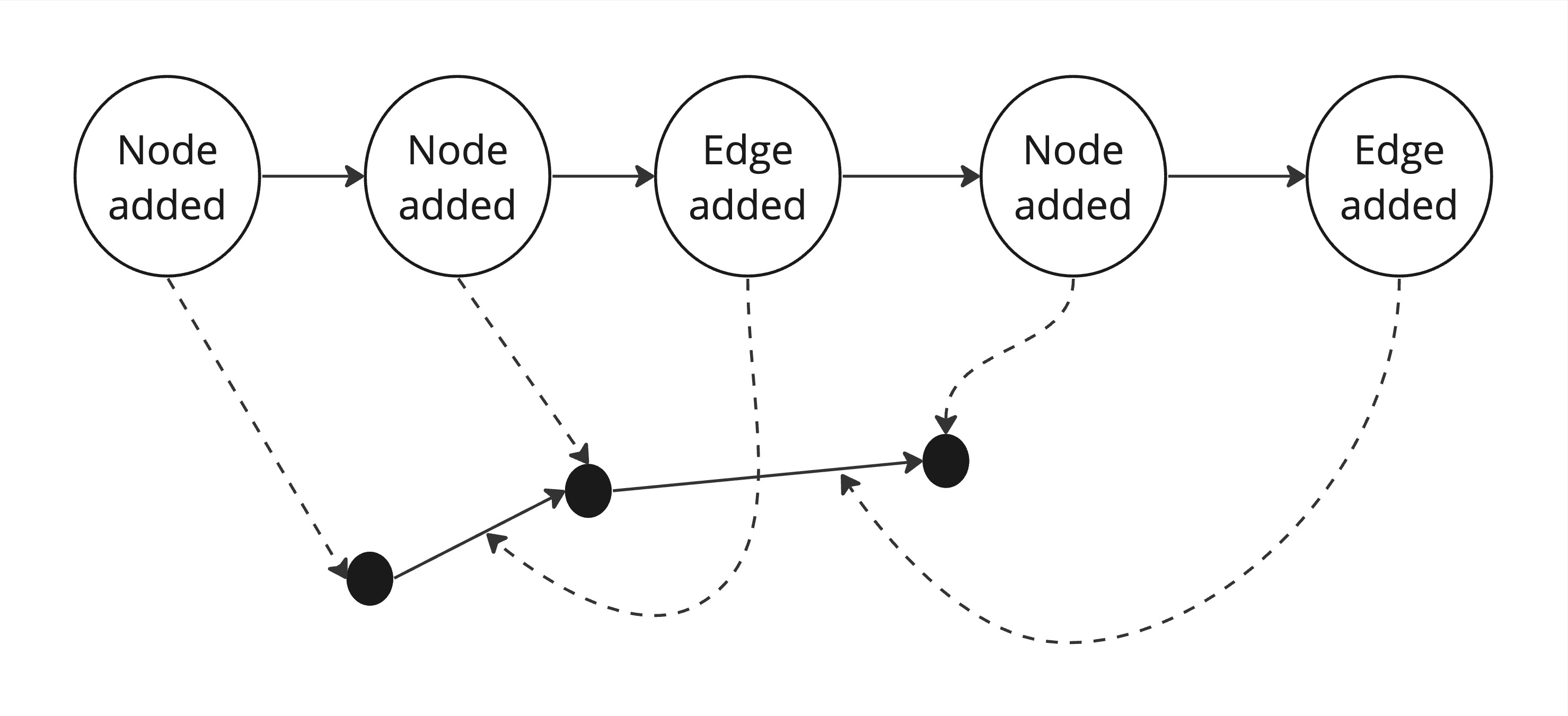
To keep it all functional, I use a lesser-known fp-ts-stream library. It has a similar API to fp-ts but does it lazily. Pure Generators could be used for this purpose, too (they are used in fp-ts-stream internally).
As a bonus, the generation process feels much faster when I see a loading indicator.
Monorepo and web workers
This is the easiest part, really.
I use the generator code on the backend, but I also want to show the generator to you.
First, I tried to generate graphs on the backend and send them through API. This is the obvious solution.
I found that not only could the generated graphs be quite large JSONs (so, network load), but also, I don’t have proper streaming (which could be solved with WebSocket, which is another way of doing it).
I found, though, that the Web Worker generates the graph much faster (or rather, perceivably much faster - I didn’t actually benchmark it) than my API.
The Web Worker code is stupidly simple:
/// <reference lib="webworker" />
import { pipe } from 'fp-ts/function';
import * as STR from 'fp-ts-stream/Stream';
import { Seed } from '@firfi/utils/rng/seed/types';
import { GraphGeneratorSettingsInput } from '@firfi/graphgen/index';
import { getRandomFinalizedGraph } from '@firfi/graphgen/getRandomGraph';
onmessage = (
e: MessageEvent<{
seed: Seed;
settings: GraphGeneratorSettingsInput;
}>
) => {
pipe(
getRandomFinalizedGraph(e.data.seed)(e.data.settings),
STR.map((e) => {
postMessage(e);
}),
STR.toArray // to actually run it
);
};
And it even handles cancellations/reinitialization with worker.terminate(); and seems to be fine about it.
To marry the backend and frontend/Web Worker code, I used an Nx monorepo. It fits at least TypeScript projects quite well, and codesharing is incredible.
Now, now, let’s see what we’ve made16
Let’s review.
We’ve learned:
-
That it’s possible to make a TypeScript isomorphic with a monorepo17
-
That perceived performance and UX can be improved by having a loading indicator for long-running tasks, which can be made possible with lazy computations.
-
That determinism can help with various advanced tasks such as property-based testing and game networking.
-
That pseudo-random number generators take a special place in deterministic computations.
-
That there are algorithms for quasi-realistic graph generation.
-
And that Newtype is a nice pattern but not so well supported in TypeScript.
-
We also learned the Dungeons and Dragons 5E advantage/disadvantage rule and that it might even help you with weighted random number generation… sometimes.
And we have established software foundations for continuous property-based testing using random graph structures.
That’s it! Have fun and enjoy!
https://graphgen-ts.apps.loskutoff.com/
Notes
Footnotes
-
Well, the real case differs a bit from this extended metaphor, but we’ve framed it in this way to keep our NDA intact. ↩
-
According to my own benchmarks, i.e., in my opinion ↩
-
https://en.wikipedia.org/wiki/Profiling_(computer_programming) ↩
-
I don’t go further into this as I found it less important later. It was an important starting point, though. ↩
-
In my experience, at least, especially when you compare with Haskell. Even Elm is not lazily evaluated ↩
-
Which is also the core game mechanic for wildly popular videogame Baldurs’ Gate 3 https://store.steampowered.com/app/1086940/Baldurs_Gate_3/ ↩
-
I’ll take this opportunity to plug Cory Spencer’s article about Minecraft skin generation with AI ↩
-
Deterministic computations, apparently, are a big deal in videogame network programming ↩
-
Node is single-threaded but, if any asynchronous computation is introduced, concurrent calls will still mess each other up ↩
-
Well, unless you are an Elf or a Half-Elf of Xanathar’s Guide to Everything with the trait Elven Accuracy, when you are able to roll 3 advantage rolls instead of 2 in some situations. ↩
-
But really, you can just use workspaces ↩